实验原理

电子是一种构成物质的基本粒子，决定了物质的物理及化学性质，如材料的吸收及折射特性。超快时间分辨吸收和折射探测系统原理为利用光与物质的相互作用后吸收、折射等变化过程，对无法直接观察的电子的运动过程进行超快时间分辨的探测，从而获得电子运动所带来的实时影像。

强激光下的时间分辨泵浦探测技术可以研究强光作用下材料内电荷变化的瞬态过程。在该技术的基础上发展了许多具有划时代意义的探测技术，如时间分辨光谱技术，超快时间分辨光电子显微镜技术等。1999年诺贝尔化学奖授予美国加州理工学院的物理化学和化学物理学家Ahmed H Zewail教授,以表彰他在利用飞秒时间光谱技术研究化学反应方面的开拓性工作。超快时间分辨光电子显微镜已被广泛用来探测表面形貌、化学反应、薄膜生长等。另外脉冲宽度是脉冲激光器的重要性能指标，利用时间分辨泵浦探测技术可以测量ps和fs的脉冲宽度。

1.超快时间分辨泵浦探测光路（同时含吸收和折射）

超快时间分辨泵浦探测光路如图1（a）所示。利用一个分束镜BS₁，激光脉冲被分成了两路：泵浦系统及T-PO探测系统。泵浦光路主要由两个反射镜M₂、M₃，直角棱镜，凸透镜L₂组成，直角棱镜装置在一微动平台上，可以前后平移以改变泵浦光的延迟时间；探测光路主要由反射镜M₁，相位物体PO，凸透镜L₁，分束器BS₂，小孔径光阑，探测器D₁和探测器D₂组成；泵浦光路与探测光路同时聚焦于待测样品上。

探测光路经过反射镜M₁改变方向，透过相位物体PO后由凸透镜L₁聚焦到待测样品上，经过分束器BS₂后，分成两束光，透射的一束经小孔后由探测器D₂接收，反射的一束经凸透镜L₃会聚后由探测器D₁接收；泵浦光经过反射镜M₂，直角棱镜，反射镜M₃构成的延迟平台，由凸透镜L₂聚焦到待测样品上，使待测样品处于基态的粒子受到激发跃迁到激发态，粒子布居数分布的变化对探测光路的吸收和折射产生影响，又由于粒子布居数随时间是不断变化的，前后平移直角棱镜可以对不同时刻的探测光路产生不同的影响，并被探测器接收。

在实验过程中，通过使用一个半波片将泵浦光的偏振状态和探测光的偏振状态调成垂直或平行。在探测光分支中凸透镜L₁的前焦面上放置一个如图1（b）所示的相位物体PO。PO就是在透明的介质上沉积一个半径为Lp的玻璃片。透明介质具有厚度和线性折射率，因此，对入射光具有一定的位相延迟。PO正常情况下放置在透镜L₁的前焦面上，这样做的目的是为了计算处理方便。在远场处小孔的半径和传播到远场的的探测光中的PO衍射光斑的半径相同。一个时间延迟线引入到泵浦光支路中，两束光在样品池以一小角度重合。探测光的光斑半径小于泵浦光的光斑半径，以上两点条件保证了探测光在薄样品池中探测到一个经过均匀激发的区域。泵浦光经过之后，探测光能量随延迟时间的改变的实验结果被记录下来。

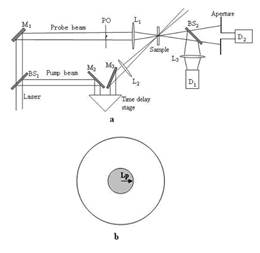
图1 (a) 瞬态非线性折射仪光路。BS，分束镜；M₁-M₃，镜面；L₁-L₃，凸透镜； D₁-D₂，探头。(b)PO示意图。

2.超快时间分辨泵浦探测技术原理

泵浦探测系统中，激光器出射激光由分束镜分为两束，一束为泵浦光，一束为探测光，两束光之间通过一个时间延迟系统，可以调节泵浦光和探测光之间的延迟时间。对于不同的光学非线性机制，电子在不同能级上有着不同的形成时间和恢复时间，可以利用这一特点研究和区分材料的光学非线性响应机制。

泵浦光与探测光作用在材料上相同的区域，泵浦光的光强较强，它的作用是激发材料的光学非线性。当泵浦光入射到待测样品上时，样品在强光照射下产生非线性光学响应，材料的性质发生改变，因此能够对经过其中的探测光形成调制。通过调节泵浦光和探测光的光程差（延迟时间差），在不同延迟时间下测量样品的透过率，即可研究该材料的非线性动力学过程。实质上，时间分辨泵浦探测技术就是将系统中空间变化转化为时间变化的一个过程，时间分辨吸收曲线或折射曲线的宽度即为泵浦光和探测光两个激光脉冲相关卷积的结果，假设所使用的材料非线性吸收机制为双光子吸收或超快克尔响应，则从而测量出激光的脉冲宽度。

（1）激光入射

泵浦光在样品池表面的初始光强分布可以表示为：

 

其中，是泵浦光在位置z处的光斑半径。Z是样品离开焦点的距离，是光束的衍射长度，是泵浦光在焦点的光斑半径，即束腰，是焦点处轴上的峰值光强，是泵浦光和探测光之间的延迟时间。

 

其中，r是横向极坐标，是高斯光在系统入口处的束腰，表示激光的电场分布，是激光脉宽(FWHM)。

圆形的PO的半径为Lp的范围内具有统一的线性位相，对于的情况，相位物体的线性透过率可以表述为，其余的情况为1。在我们的实验情况下，由于解析表达式，我们将探测光光场从相位物体传播到凸透镜L₁。电场在PO的出射面上的表达式可以表示为：

 

光场从相位物体传播到小孔A的过程需要三步菲涅尔衍射积分来完成。

（2）样品前激光分布

对于PO放置于透镜的前焦面的情况下，在凸透镜的前焦面上，探测光的光场可以表示为：

 

其中，d=f是传播距离，是在该平面上的极坐标，是一类零级贝塞尔函数，在傍轴近似情况下，由于透镜而产生的位相可以表示为。那么，在透镜L₁的后表面上，探测光的光场的振幅可以表示为：。第二次传播过程是由透镜的后表面传播到样品所在位置，即透镜的后焦平面上，传播距离为d=f。

（3）光与物质的相互作用（宏观）

假设探测光在非线性样品前表面的光场分布可以表示为E_p。激光入射到样品中，考虑样品为薄非线性介质，同时在慢变振幅近似情况下，我们可以将光束的传播方程分解为两个方程，一个表征光强的变化，另外一个表征位相的变化，值得强调的是，该方程是整个时间超快分辨测量技术的核心，需要获得的就是和这两个物理参量的具体表达式，而这两个物理量的大小由材料内部电子的运动轨迹息息相关，这样就可以通过实时观察透过材料的吸收曲线和折射曲线就可以确定材料内部电子的踪迹。这两个方程我们可以表示为：

 

这里，和表示探测光的光强和位相，是探测光在样品中的传播距离。和分别表示非线性吸收系数和非线性折射率的改变，这里它们都是由于泵浦光的存在引起的。通过对探测光强进行时间和空间的双重积分，可以给出一个和探头D₁相关联的能量。假设透过样品后光场为。

（4）透射光的计算

最后一次菲涅尔衍射是从样品的后表面传播到小孔光阑所在位置，传播距离d=D。D表示从样品后表面到小孔所在平面的距离。由此，我们可以推导得到小孔光阑所在平面的电场分布。在远场处的小孔光阑的半径经过调整，和探测光在衍射传播过程中PO的衍射光斑半径相同。然后，在对远场处小孔所在平面的光场分布进行时间和空间的双重积分，我们就可以得到和位于小孔后D₂相关联的能量。

小孔A处的光场可以通过菲涅尔衍射积分得到：

 

这里，D是小孔到焦平面的距离，r₂是平面内的半径坐标。

类似的，在线性的情况下，我们也可以得到小孔处的光场，定义为。将光强对脉冲宽度和小孔半径积分就得到了探测器D₂探测到的能量。于是归一化的非线性透过率可以表示为

 

当r_a趋于无穷大时，归一化的非线性透过率仅仅和非线性吸收有关。通过对实验得到的归一化的非线性透过率进行数值拟合可以得到非线性吸收系数和非线性折射系数。同时，如果T_nor大于1，非线性吸收就为饱和吸收，非线性折射系数为正，T_nor小于1时，非线性吸收为反饱和吸收，而非线性折射为负。

（5）光与物质相互作用-材料的非线性吸收及折射理论（微观）

1）激发态吸收五能级理论

在材料的超快吸收及折射研究方面时间分辨泵浦探测技术是最佳的测检手段之一。能级模型则是与时间分辨有关的材料吸收和折射性质分析的理论基础，五能级模型被公认为能级模型的标准。通过五能级模型，可以获得材料各个能级中粒子数随时间分布的情况，而材料的吸收和折射性质是与能级在一定时间内不同能级的粒子数息息相关的，不同能级上的吸收截面不同，从而导致在泵浦光作用到样品上后，吸收和折射的性质随时间变化的情况，从而获得电子随时间变化的踪迹。

在旋转波和慢变振幅近似下可以从用密度矩阵的运动方程得到粒子数的速率方程。一般而言，光场与团簇分子相互作用时可以用包括三个单重态S₀，S₁，S₂和两个三重态T₁，T₂的五能级结构图2加以说明。

 

图2 团簇分子五能级模型

按偶极跃迁选择定则，三重态和单重态之间的跃迁是禁止的，但对一些特定的大分子，由于自旋-轨道耦合增强而使系际跃迁量子产率较大，特别是金属原子和其它一些重原子耦合到分子结构中，能够使能量相近的单重态和三重态的波函数重叠，从而使系际跃迁时间变短。

图中的多条细线表示每一电子能级的振动能级，较高的振动能级由于寿命非常短，实际上可不考虑；带箭头的直实线表示低能级到高能级的受激吸收；虚线表示高能级受激辐射跃迁低能级，这种跃迁的荧光量子速率较小，这里也被忽略；波浪线表示高能级到低能级的弛豫过程。

处于单重态基态的分子，在入射光子的作用下，以速率向第一单重激发态S₁跃迁。处于激发态S₁的分子有多种跃迁途径，以速率向第二单重激发态S₂跃迁，这个过程吸收一个光子；以速率弛豫到基态S0和以速率系际窜越到能量较低的第一三重激发态T₁。在T₁态的分子受激吸收到第二三重激发态T₂的速率是，系际窜越到S₀的速率为。第二单重激发态S₂则以速率弛豫到S₁。在T₂态的分子弛豫到T₁的速率为。粒子数变化的动态过程由下面的速率方程描述：

 

公式中I即为泵浦光Ie，, , , 和分别为能级, , , 和的粒子数密度，为总的粒子数密度，它们是时间和传播距离的函数；是入射光强；, 和分别为能级, 和的分子吸收截面；和分别为能级和的寿命；为到的驰豫时间；为到系际跃迁时间，在到跃迁过程中电子的自旋发生反转；为到系际窜越的时间，到可通过跃迁-辐射磷光也可通过无辐射跃迁来实现，由于从到系际窜越的速率远大于到跃迁速率，即，重金属原子可使分子的系际窜越速率大大增加。

对速率方程(5) 进行分析就可以得出有关非线性吸收基本规律。假设入射光为连续波或者脉宽足够长，那么一开始，由于低能级的粒子数远远大于高能级粒子数，低能级向高能级跃迁的粒子数远大于高能级向低能级弛豫的粒子数，此时高能级的粒子数不断增加，低能级的粒子数不断减少；低能级的粒子数减少，向高能级的跃迁几率减小，高能级粒子数增加，向低能级弛豫的几率也随着增加，而总的粒子数不变，所以可以预料在一段时间以后，各能级粒子数分布达到动态平衡，在激光作用时间内基本上不变。若入射光的脉宽很小，则各能级的粒子数将不能达到动态平衡，此时我们分析材料的非线性应采用动态方法，求解出各能级粒子数随时间的变化，然后得出非线性吸收系数随时间的变化。

2）基于激发态光学非线性的吸收及折射理论

如一样品的光学非线性为激发态非线性，则样品对光强的非线性吸收系数和非线性折射率变化为

 

 

这里为各个能级的吸收截面，为各激发态能级与基态能级的折射体积之差。对速率方程(5)进行分析就可以得出有关非线性吸收和折射的基本规律。

激光在样品中传输的光传播方程为

 

利用式(5), (6)和(7)可得到任意材料的非线性吸收及折射性质。

上面已经提到，当入射光的脉宽很小，各能级的粒子数将不能达到动态平衡，此时我们分析材料的非线性必须采用动态方法，求解出各能级粒子数随时间的变化，然后得出非线性吸收系数随时间的变化。在进行实验时，我们使用的脉冲激光器脉冲都很小，一般为皮秒或纳秒量级，因此在对实验数据拟和时必须采用动态方法，对方程(5), (6)和(7)进行数值求解，从而得到样品的非线性吸收。再对公式（8）进行求解就可以获得超快时间分辨非线性吸收和折射引起的吸收曲线和折射曲线。在一定的条件下可以对上面的五能级模型进行简化，从而节省数值计算的时间。

3）双光子诱导激发态理论

图3所示为双光子诱导激发态的三能级模型。其中，S₀表示化合物分子的基态，S₁、S₂分别表示化合物分子的单重态第一激发态和单重态第二激发态。各代表能级中的粗实线表示该能级的电子能级，细线则表示同一级电子能级上的振动能级，带箭头的粗实线表示从低能级到高能级的受激跃迁，带箭头波浪线代表分子在能级上的弛豫过程。在热平衡状态下，绝大部分分子都布居在基态S₀，而在作为激发态的高能级，分子的布居数很少，因此，在平衡状态下，可以近似认为分子全部布居在基态。前面，我们已经提到，样品在800nm波段没有线性吸收，因此，我们认为分子位于激发态上的粒子数布居是由双光子吸收引起的。这样，在外来光场的作用下，平衡状态下的分子受到入射激光的激发，就会同时吸收两个光子从基态S₀跃迁到第一激发态S₁的振动能级上，然后迅速驰豫到S₁上。到达激发态S₁上的电子有两种跃迁途径，一种是再吸收一个光子跃迁到更高的能级第二激发态S₂的振动能级上，然后迅速驰豫回S₂，最后经过一定时间的驰豫，无辐射跃迁回落到第一激发态S₁上。另一种跃迁途径是经过一定的时间驰豫，无辐射跃迁到单重态S₀上。

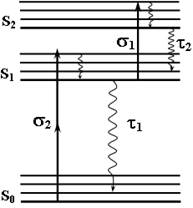
图3 双光子诱导激发态三能级模型

由于振动能级之间的跃迁驰豫时间很短，远远小于激光脉宽，我们可以近似认为振动能级上的粒子数布居为零。这时，各能级布居数的动态变化，可以用速率方程来描述：

 

其中，，，，分别为能级S₀，S₁，S₂上的粒子数密度，为基态的双光子吸收截面，为第一激发态的吸收截面，为第一激发态的寿命，是第二激发态的寿命，为样品内的光强，是普朗克常数，是入射激光的角频率。

（6）超快时间分辨吸收及折射归一化透过率曲线的形成

在样品前表面上泵浦光和探测光的光强分布为：

 

 

泵浦光通过样品每一层后的光强变化为：

 

探测光在这一时刻通过样品每一层后的光强及相位变化为：

 

其中和分别为探测光和泵浦光的光强。分别为探测光和泵浦光在焦点处的束腰半径，,() 为探测光和泵浦光在离焦点位置处的光束半径的大小， 为衍射长度，为轴上焦点处的峰值光强，其可由公式，得到， () 脉冲能量， 为脉冲宽度(HW)。为泵浦光和探测光之间的时间延迟。为基态的吸收截面，和分别为激发态S₁和T₁的吸收截面； 和 分别为态S₀，S₁，S₂，T₁和 T₂上的实时粒子布居数，由公式（5）、（9）或（11）获得； 为系间跃迁的时间; 脉冲光在样品中传播的位置。

需要注意的是在泵浦-探测实验中，探测光的能量要比泵浦光的能量要小得多，一般探测光的光强大约为泵浦光的1/100，因此在搭建光路时，要将探测光的光强尽量调低。因此探测光对粒子布居数的影响可忽略不计，如公式(5)所示。

各个能级上的粒子布居数的变化由泵浦光的光强，各个能级的吸收截面，以及各个能级的寿命决定，必须强调的是，每一个能级对吸收的贡献，取决于这个能级的粒子布居数和吸收截面的大小。

通过对探测光强进行时间和空间的双重积分，可以给出一个和探头D1相关联的能量。最后一次菲涅尔衍射是从样品的后表面传播到小孔光阑所在位置，见公式（6），传播距离d=D。D表示从样品后表面到小孔所在平面的距离。最终可以推导得到小孔光阑所在平面的电场分布。在远场处的小孔光阑的半径经过调整，和探测光在衍射传播过程中PO的衍射光斑半径相同。然后，在对远场处小孔所在平面的光场分布进行时间和空间的双重积分，我们就可以得到和位于小孔后D₂相关联的能量。

图4 半导体ZnO的瞬态光学非线性测量结果